Features are extracted from the EEG signals that aim to capture the important, event-discriminatory, information. This allows for reduction in the size of the data set without the loss of information, resulting in shorter training times and potentially better classification performance.
Epoching
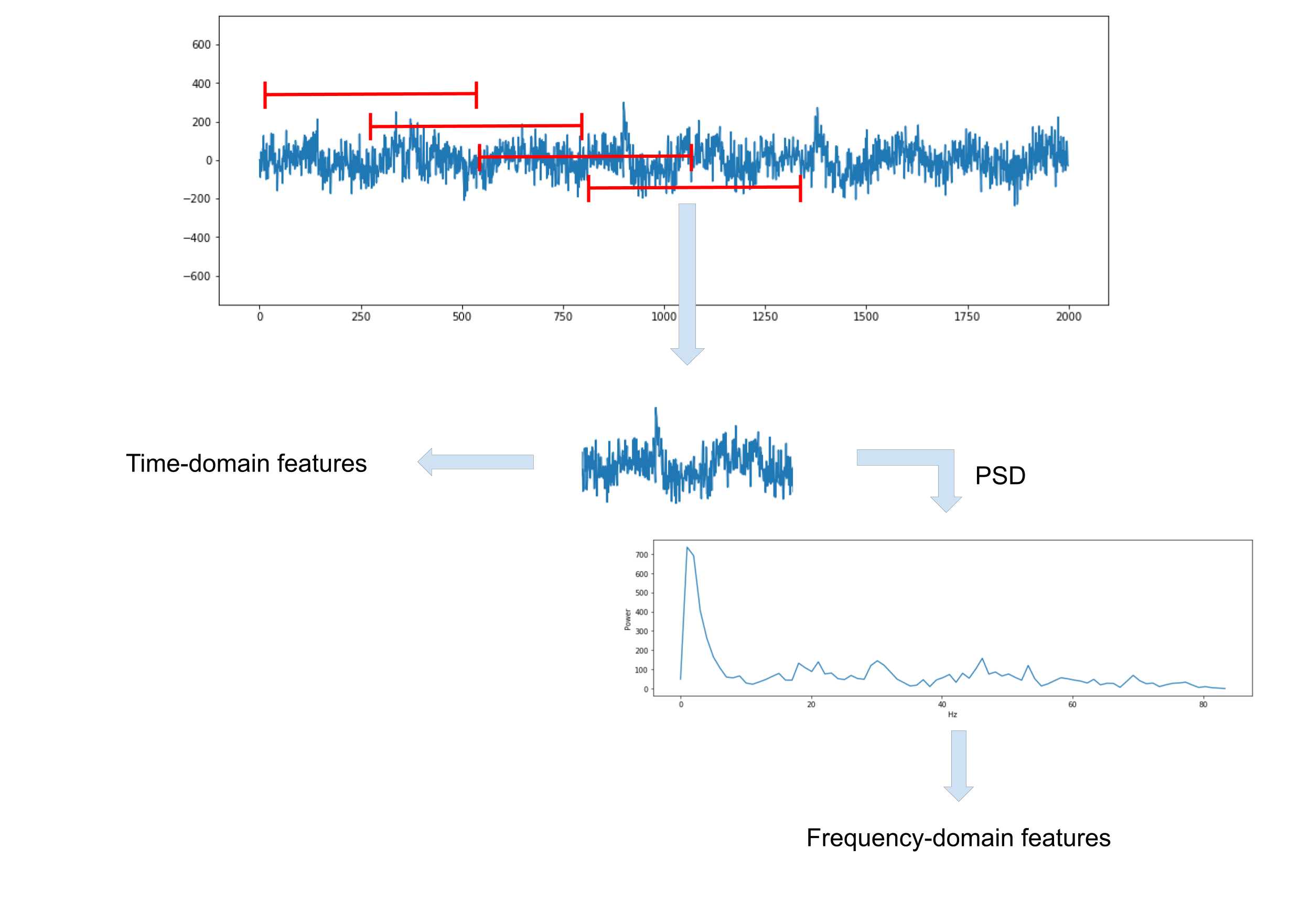
The signals are split into segments of data known as epochs, from which a set of features are extracted. A sliding window is used to pass through the data, extracting features as it goes. The length of the window, dictating how much previous information is useful for predictions, is an important parameter affecting classification performance. Window lengths of 0.25, 0.5, 1 and 2 seconds are tested, all with 50% overlap. The set of features extracted from a window take the events label of the final sample in that window.
Time-Domain Features
The first type of feature extracted from each epoch are temporal features, describing the EEG signal amplitude over time. Simple statistical properties - maximum, minimum and mean absolute value, and Hjorth parameters - activity, mobility, complexity, are computed.
Frequency-Domain Features
Spectral features are also extracted from the signals. For each epoch the power spectral density (PSD) estimate, describing the power of the signal at different frequencies, is computed. Welch’s PSD estimate computes the modified (window function to reduce spectral leakage) periodogram across overlapping segments of the EEG signals, reducing the variance of the estimate over the periodogram and Bartlett’s method (non-overlapping segments). Welch’s PSD estimate is computed with SciPy’s welch function, with 50% overlap between segments and a Hann window function. The maximum power and the frequency at which maximum power occurs are extracted from each PSD, in addition to the average power across each quarter of the PSD (average across each quarter used rather than the PSD itself to reduce number of features).
Principal Component Analysis
Extraction of multiple features from multiple channels of EEG data results in a highly dimensional feature space, inevitably containing redundant features that can worsen classification performance and increase training times. It can therefore be useful to reduce the dimensonality of the feature space by keeping the useful information whilst throwing out the redundant information.
Principal component analysis (PCA) is one such technique that can be used for dimensionality reduction. In PCA, orthonormal vectors (the principal components (PCs)) are computed, with the first one being the direction in the feature space with maximal variance. The second PC is therefore the vector with maximal variance that is also orthogonal to the first PC and so on for n PCs for an n-dimensional feature space. By selecting a number of PCs that explain some large proportion of variance in the feature space, and dropping those that account for little variance, the dimensionality of the feature space is reduced when transformed with the kept PCs. PCA is implemented with scikit-learn, and the number of features kept is set as n_components=0.95, using the number of components that cumulatively explain 95% of the variance in the feature space. PCA is applied after normalisation as it is sensitive to scale of features.